At Hannover Messe a few years ago, SKF announced the launch of the SKF Universal Bearing Life Model, an innovative model that helps engineers take a more realistic approach to calculating the rated life of bearings.
The model is a major breakthrough for the bearing industry, allowing ancillary customers and end users to play an important role in better matching bearing products to applications, thereby increasing equipment life and reducing operating costs.

At Hannover Messe, SKF presented the EnCompass field performance programme and launched the SKF Universal Bearing Life Model.
Developed as part of SKF’s EnCompass field performance programme, the life theory successfully separates the surface fatigue model from the sub-surface fatigue model, leveraging the strengths of the existing bearing life theory (developed by SKF and widely used for more than 30 years), and providing new insights into calculating the rated life of a bearing by introducing additional parameters.
The Universal Life Calculation Concept promotion in Hanover included two days of live interviews with experts, demonstration software showing the calculation methodology, and one-on-one interaction with customers and journalists. The conceptual model was well received by the audience and customers and renewed interest in the calculation of rated bearing life.
Next, we will present the principles of the new model in two parts.
The power of tribology
To date, rolling bearing life calculations have been based on an engineering model of equivalent stresses that takes into account equivalent stresses originating below the contact surface that are applied to the stress volume of the rolling contact.
For many years, surface-originated fatigue has been considered to be due to poor lubrication or contamination, and the effect of this form of failure on life has been realised by adding a correction factor to the total equivalent stress in the rolling contact and incorporating it into the bearing life calculation formula.
In this paper, we address this surface fatigue failure problem by developing a generalised rolling contact life method. In this method, surface-originated damage is explicitly formulated in the basic fatigue formula for rolling contacts. This new formula better reflects the tribological properties of rolling bearings in rated life calculations.
In addition, it provides a better understanding of the surface fatigue life that plays a major role in the field performance behaviour of rolling bearings. This general approach serves to explain bearing friction while discussing the contradictory fatigue mechanisms that occur on the surface and subsurface inside rolling bearings.
With proper use and good lubrication, rolling bearings are becoming increasingly reliable due to correct practice and the successful understanding and application of traditional rolling contact fatigue mechanisms.
At the same time, improvements in steel purity and processing quality, combined with reliable life calculation methods, have also been an important part of the increase in bearing reliability.
However, the trend towards miniaturisation of industrial equipment and higher demands on performance efficiency in the field have brought about more demanding application conditions for rolling bearings, especially on the contact surfaces, which is why most bearing failures are related to surface fatigue [Literature 1].
In order for bearings not to become a bottleneck in further improving the performance of modern equipment, surface friction properties need to be better assessed when it comes to bearing performance. Over the last decade, SKF has made substantial progress in the area of surface life modelling [Literature 2-8].
This culminated in separating surface fatigue from the life theory of sub-surface fatigue through the introduction of the SKF Generalised Bearing Life Model and incorporating this knowledge into rolling bearing rating life calculations [Literature 9].
In this approach, different physical models are used for the two regions. Sub-surface rolling contact fatigue can be calculated along the lines of the classical Lundberg and Palmgren dynamic load theories [Literature 10], but when dealing with surface fatigue, a more advanced friction model is required, one that takes into account the more complex physical effects such as lubrication, friction, wear, fatigue, or galling that occur as a result of the concentration of stresses on the Hertzian contact surfaces.
This enables SKF to reflect more customised designs with special properties in bearing life calculations, which can influence the performance of the bearing in field applications. Examples include special heat treatments for bearings, advanced microgeometries, unique designs or higher quality.
Customers are able to take advantage of the different unique features of bearings in the SKF product catalogue and use them in rating life calculations. Ultimately, instead of simply selecting a bearing using the basic dynamic load rating (C), which only represents ‘sub-surface fatigue’, as is currently the case, customers will be able to take better advantage of the unique properties of SKF products and the higher quality of the products.
The new model specifically addresses the ageing mechanism of bearings, while friction on raceway surfaces will be more widely used in the development of bearing products in this more advanced version of the General Bearing Life Model.
SKF engineers will use the Universal Bearing Life Model to develop improved bearing designs for specific applications or site-specific performance requirements. In summary, the Universal Bearing Life Model represents a more modern and flexible tool for evaluating bearing performance, and is able to incorporate new knowledge and technology as it evolves.
Generic modelling approach
The present model will continue to retain the standardised probabilistic statistical approach to rolling bearing life calculation that is still in use today, which is based on two-parameter Weibull distribution theory calculations, see discussion in [Ref. 12].
Varody-Weibull [Literature 13] introduced the stochastic concept of determining the strength and fracture of a structural element in the weakest link theory of his chain model.
If a structure is composed of n elements subjected to different stress states, under different life probabilities S1, S2, … , Sn, the whole structure life probability can be derived from Eq. (1) according to the reliability product law.

Lundberg and Palmgren, in their earlier classical basic dynamic load rating formulation for rolling bearings [Ref. 10], substituted the Weibull reliability product law into Eq. (1) to derive Eq. (2) for the life function of a structure consisting of n independent physical elements, which comprises the ageing process from 0 to N load cycles.
Considering that G represents a function of material ageing caused by the cumulative effect of load cycles (fatigue), the volumetric parameter V can be divided into two or more damage originating factors for independent structures.
Thus, different regions can be characterised by different material ageing functions that describe different (or single) material ageing processes Gv.1, Gv.2, … , Gv.n, and their combined effect on the overall structural lifetime can be expressed by Equation (2). However, considering that now there are only two zones, one for the subsurface (v-zone) and the other for the surface (s-zone), Eq. (3) can be derived.
Following [Ref. 14], the fatigue damage volume integral Eq. (4) can be obtained using the stress amplitude σv generated in the Hertzian stress region.
where c and h are exponents, e represents the Weibull slope of the subsurface, N is the contact life at the number of load cycles, z represents the depth of the subsurface to be analysed, Vv is the volume integral, σu.v is the fatigue limit at that volume, and Ā is the setting constant.
In a similar way, the surface damage function can be rewritten. If the constant ĥ is substituted for the surface damage probability constant B ̅ , Equation (5) is obtained.
Where m is the surface Weibull slope, A is the surface integral, σu.s is the fatigue limit of the surface, and B ̅ is the setting constant.
In the surface damage equation (5), the surface stress σs must be derived from the actual surface shape of the contact surface and the friction stress.
Now, by combining Eqs. (4) and (5), with Eq. (3), it is possible to obtain the contact life equations for the separate terms of the surface and subsurface. Note that it is possible to relate the life in revolutions to the number of load cycles by means of L = N/u, where u is the number of load cycles per revolution, taking into account that the two Weibull slopes are very similar e = m, which is the relevant surface fatigue model for bearings, and finally obtaining Eq. (6).
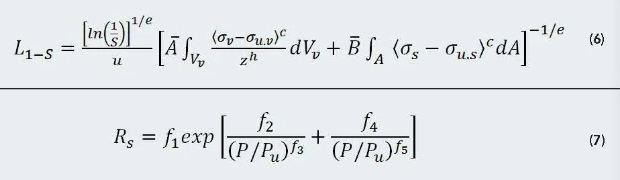
This is the basis for a bearing life model that explicitly separates the surface terms from the subsurface terms. The subsurface term, represented by the volume integral, can be calculated by the traditional Hertzian rolling contact fatigue method in [Ref. 14].
The surface term represented by the area integral, on the other hand, includes many of the frictional phenomena that characterise the life of raceway surfaces in a more compatible way in the new life theory.
Of course, the development of the new model required the use of a more advanced data model. In fact, it needs to describe more complex interactions between two ageing mechanisms with contradictory properties.
For example: i) surface fatigue combined with light wear, ii) evolution of indentation damage, iii) friction chemistry interactions, and many other factors. The following diagram demonstrates the main conceptual principles of the Universal Bearing Life Model.
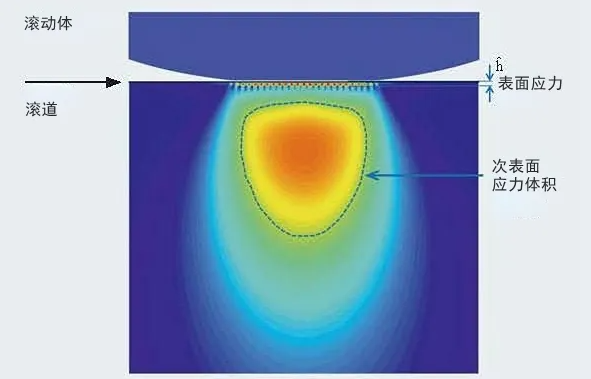
Separation of surfaces and sub-surfaces as proposed by the generic bearing life model.